Functions for caching and calculating Wigner d and D functions. More...

#include "Constants.h"
#include <complex>

Namespaces
	yap

Functions
const double	dFunction (unsigned twoJ, int twoM, int twoN, double beta)

const std::complex< double >	DFunction (unsigned twoJ, int twoM, int twoN, double alpha, double beta, double gamma)
	Wigner D-function 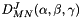$D^{J}_{M N}(\alpha, \beta, \gamma)$ .

void	cache (unsigned int twoJ)

const unsigned	cacheSize ()

Detailed Description

Functions for caching and calculating Wigner d and D functions.

Author: Daniel Greenwald, Johannes Rauch

Calculation is based on M. E. Rose's Elementary Theory of Angular Momentum (1957):

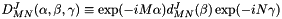
$D^{J}_{MN}(\alpha, \beta, \gamma) \equiv \exp(-iM\alpha) d^{J}_{MN}(\beta) \exp(-iN\gamma)$

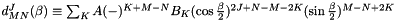
$d^{J}_{MN}(\beta) \equiv \sum_{K} A (-)^{K+M-N} B_{K} (\cos\frac{\beta}{2})^{2J+N-M-2K} (\sin\frac{\beta}{2})^{M-N+2K}$

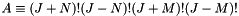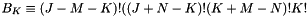with $A \equiv (J+N)!(J-N)!(J+M)!(J-M)!$ and $B_{K} \equiv (J-M-K)!((J+N-K)!(K+M-N)!K!$ .

The limits on K are governed by the factorials, since 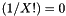$ (1 / X!) = 0 $ if $ X < 0$ .

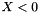We only cache matrix elements with M in [-J, J] and N in [-J, min(0, m)]. This amounts to the lower triangle and the diagonal without the bottom right corner. The uncached matrix elements are given by the by the symmetries

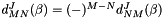
$d^{J}_{MN}(\beta) = (-)^{M-N} d^{J}_{NM}(\beta)$
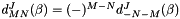
$d^{J}_{MN}(\beta) = (-)^{M-N} d^{J}_{-N-M}(\beta)$

Namespaces

Functions

Detailed Description